最高のコレクション 都 道府県 覚える 方法 777977

都道府県の覚え方 小学生 中学生の勉強
都 道府県 覚える 方法
都 道府県 覚える 方法-
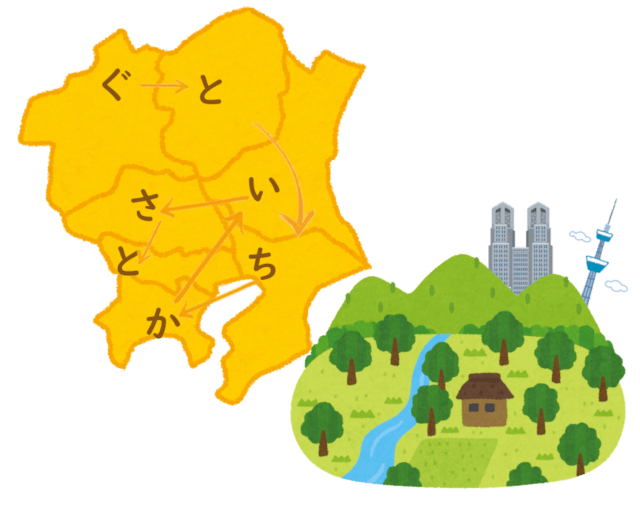



都道府県の覚え方にはコツが必要 おすすめ本と語呂合わせを紹介 バレエ男子の中学受験への日々




都道府県の覚え方 小学生 中学生の勉強
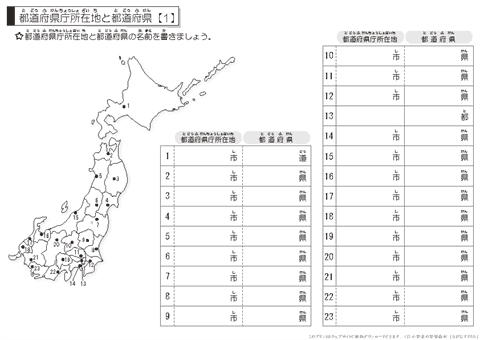



都道府県 県庁所在地 地方区分 テスト ちびむすドリル 小学生
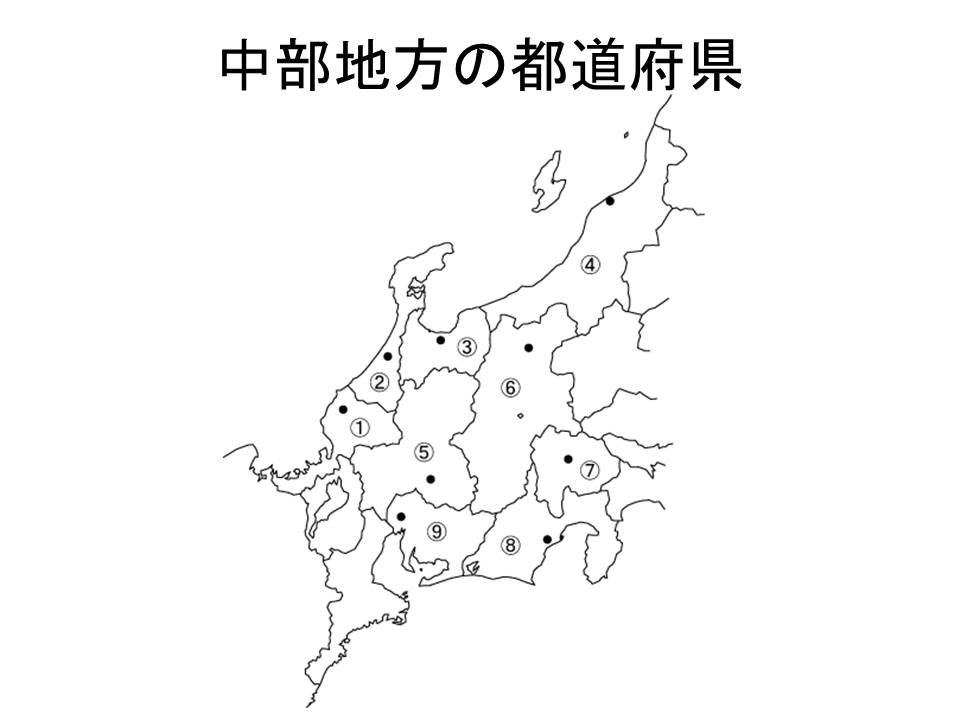



中部地方 都道府県名 県庁所在地及び場所をセットで覚えよう 社会科ポータルサイト



大至急 明日 都道府県テスト 語呂合わせで一番早く覚える 都道府県らくがき




都道府県のカタチを絵で覚える本 造事務所 イラストレーター深蔵 ふかぞう




日本地図を4つのポイントで簡単暗記 47都道府県の地方別暗記法 Start Point



都道府県の覚え方 小学生編 あそびの中で自然に身につく日本地図 ココロータス




都道府県の位置 小4テストも動画で簡単 覚えるコツとポイント わくわくhappy Time




都道府県の覚え方 語呂合わせや歌で覚える方法 Studywith 親子の学びブログ
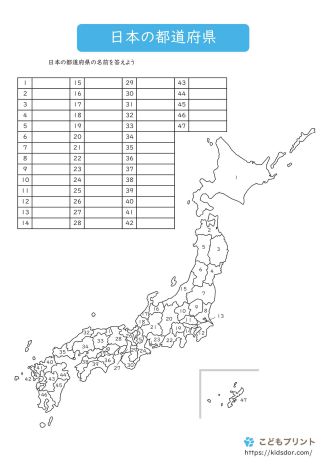



こどもプリント 都道府県の名前



中部地方の楽しい覚え方 都道府県の語呂合わせ マンガ 都道府県らくがき




小学生向け 日本地図の覚え方5選 歌 語呂合わせ アプリ そして
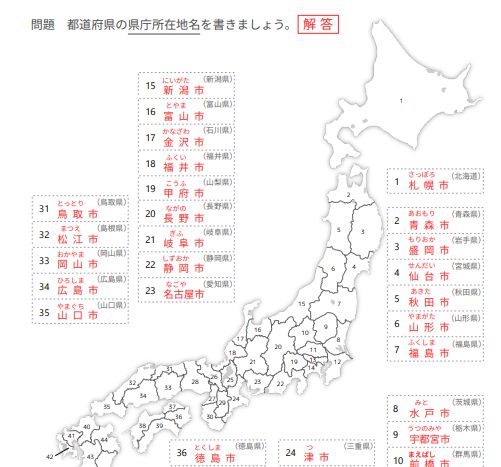



都道府県と県庁所在地の覚え方 無料のテスト アプリ クイズなど Studywith 親子の学びブログ




都道府県の覚え方 東北地方 ほるへのブログ



休校中に都道府県と世界の国をアプリで制覇



中学受験 都道府県の覚え方 効率を最大化する3つのポイント かるび勉強部屋



都道府県の覚え方 おまけで県庁所在地




日本地図47都道府県の簡単な覚え方 歌や語呂で子供と楽しく覚えよう 女性のライフスタイルに関する情報メディア
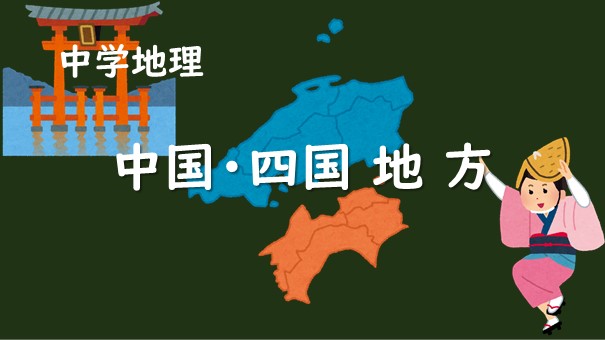



中国 四国地方 都道府県名 県庁所在地及び場所をセットで覚えよう 社会科ポータルサイト



都道府県名を覚える 1 塾の先生が作った本当に欲しいプリント 楽天ブログ



都道府県の場所や形の覚え方 パズル シルエットクイズなど Studywith 親子の学びブログ




3歳で都道府県と県庁所在地を完璧に覚えた方法 くもん地図パズルと歌 Home Learn



会場紹介 有限会社フィールドブレイン




47都道府県の暗唱 100 全員覚えることができる3つのステップ



都道府県と県庁所在地




47都道府県の覚え方 子どもも簡単に覚えられる5つの方法 Chiik




日本のすがた 都道府県庁所在地の覚え方 中学生からの質問 社会 進研ゼミ中学講座 中ゼミ




47都道府県の覚え方 子どもも簡単に覚えられる5つの方法 Chiik 日本地図 都道府県 地図
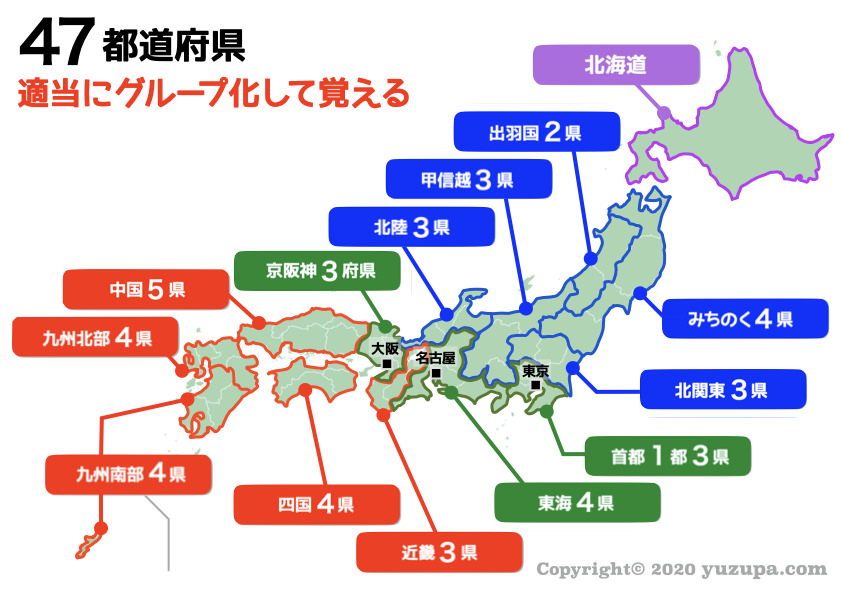



中学受験 都道府県の覚え方 効率を最大化する3つのポイント かるび勉強部屋
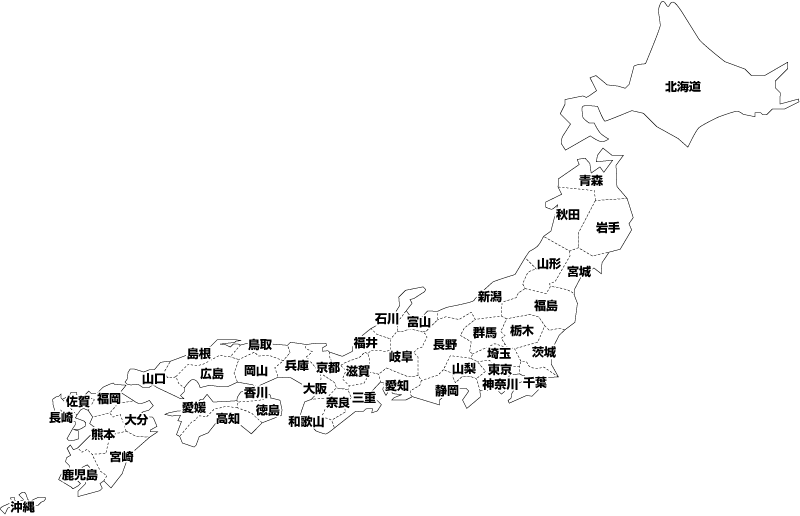



日本地図 語呂合わせで都道府県の場所を覚える方法 雨鯨のたそがれ




都道府県名を覚える 3 時空先生のドリルプリント
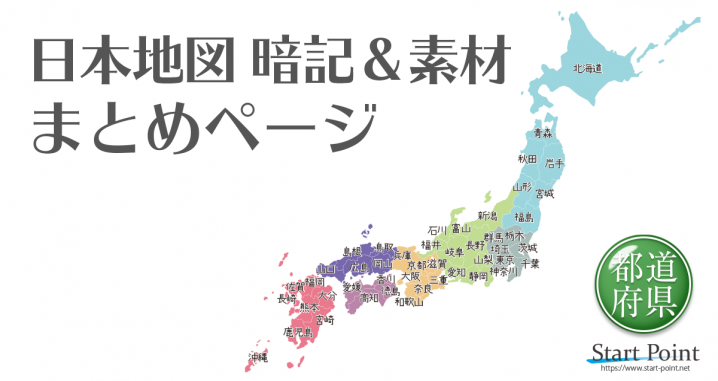



日本地図 都道府県を覚える 日本地図のフリー素材 クイズなど Start Point
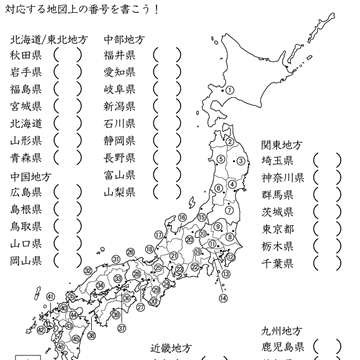



都道府県名を覚えるプリント 塾の先生が作った本当に欲しいプリント 楽天ブログ



マニヨンのナウでヤングな子育て術 全国 47都道府県の覚え方
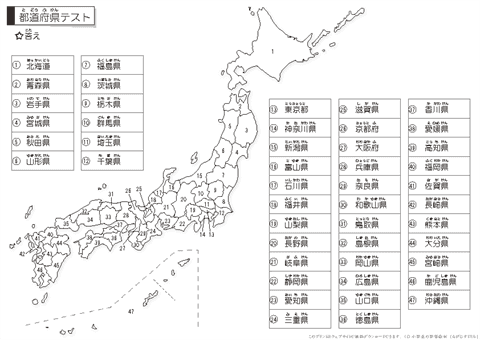



都道府県 県庁所在地 地方区分 テスト ちびむすドリル 小学生




都道府県の場所や形の覚え方 パズル シルエットクイズなど Studywith 親子の学びブログ
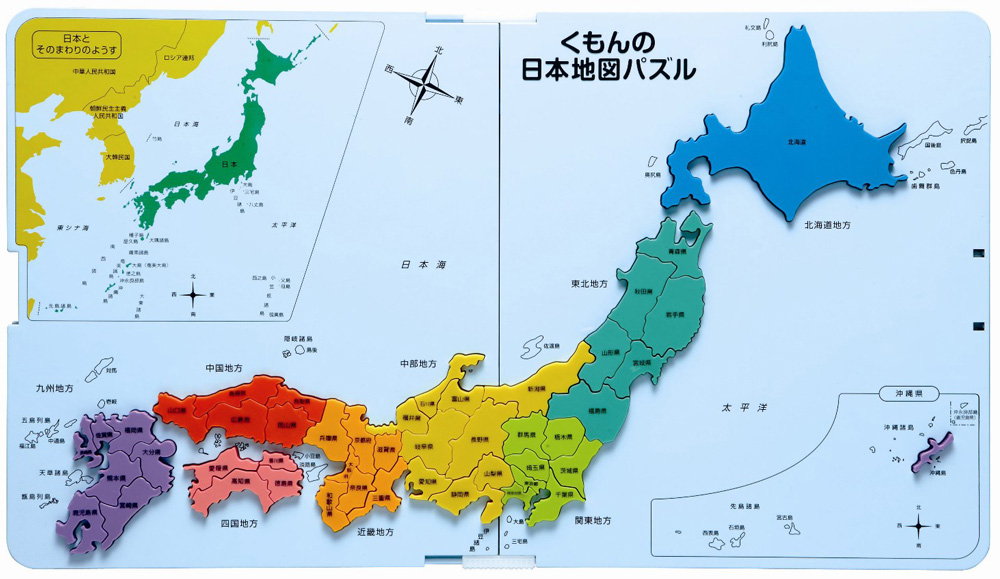



Kumon Shop




50 素晴らしい都道府県 県庁所在地 覚え方 歌 最高のぬりえ
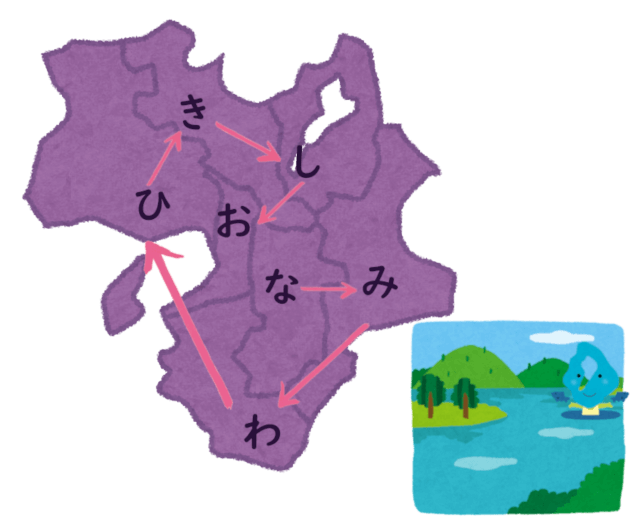



都道府県の覚え方にはコツが必要 おすすめ本と語呂合わせを紹介 バレエ男子の中学受験への日々




Amazon パズルでチャレンジ 都道府県 ジグソーパズル おもちゃ




決定版 都道府県学習かるた 幻冬舎edu




県庁所在地の覚え方 桃鉄で覚えよう たよりさん




Kaitoに47都道府県庁所在地を暗唱させてみた Youtube




都道府県の歌 中部地方 Youtube




これで完璧 絶対覚える都道府県の覚え方7つ 小学生 幼稚園むけ Youtube



都道府県の位置と形を覚えるアプリ 日本地図クイズで地理を暗記 By Kenji Kiuchi
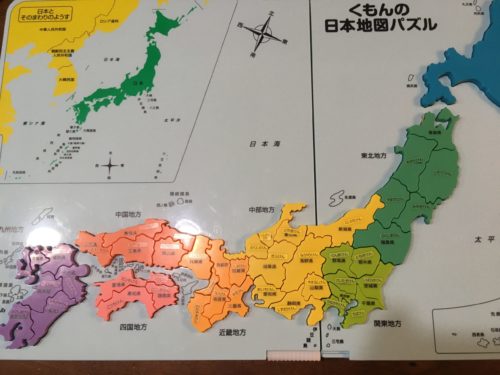



日本地図の覚え方 賢い小学生はどう覚えているのか 47都道府県だけでなく 県庁所在地などを覚える方法 くもんの日本地図パズルの知育効果は 子育てぼちぼちブログ
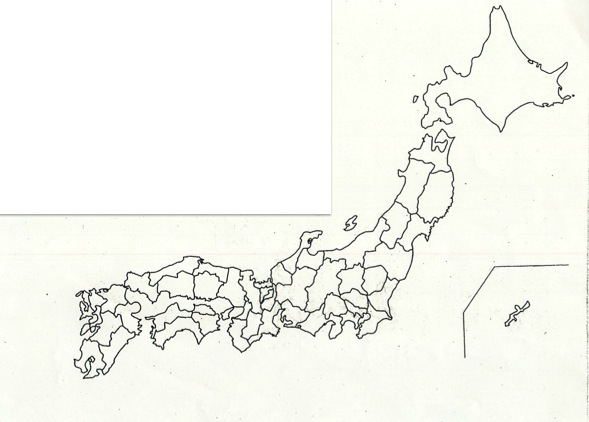



Tossランド 47都道府県の名称と位置の覚え方 2
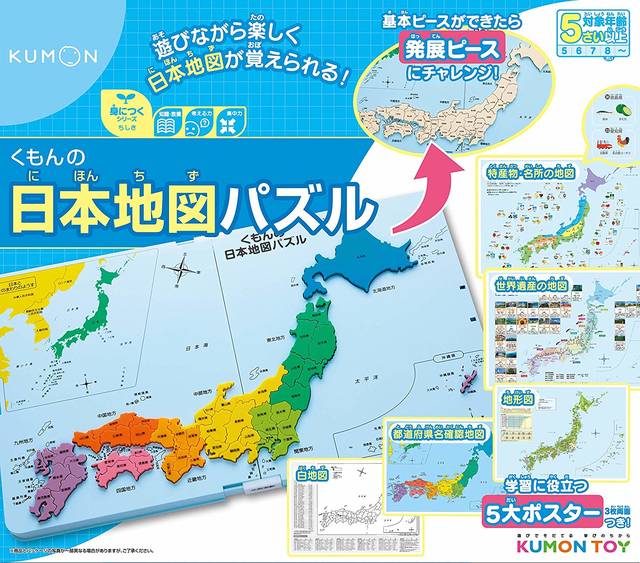



47都道府県の覚え方 子どもも簡単に覚えられる5つの方法 Chiik




3歳でもできた 超簡単な47都道府県の覚え方を大公開します かずせんブログ




ボード 子供の教育 のピン
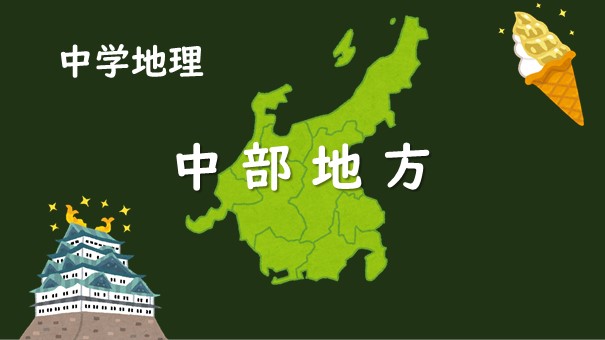



中部地方 都道府県名 県庁所在地及び場所をセットで覚えよう 社会科ポータルサイト




都道府県の覚え方にはコツが必要 おすすめ本と語呂合わせを紹介 バレエ男子の中学受験への日々



都道府県を早めに覚えると良いこと 爆走おてうブログ 中学受験25
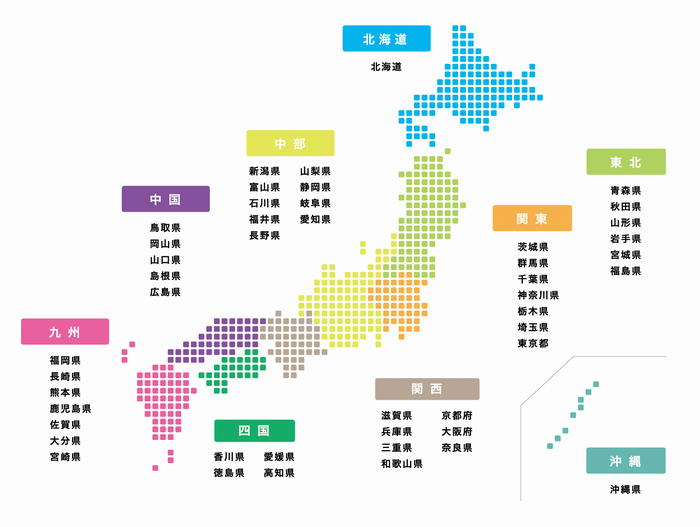



覚えにくい都道府県県庁所在地の覚え方




都道府県 日本地図クイズ 47都道府県名を答えるクイズ Start Point




都道府県の覚え方 受験やテストで失敗はこれが原因 正しい暗記法まで 幼児教育は心育てから




都道府県を覚えるのに役立つ本ー小学生の地理 しあわせ絵本生活




書いて覚える都道府県 令和版 きっずジャポニカ学習ドリル 小学館クリエイティブ編 本 通販 Amazon
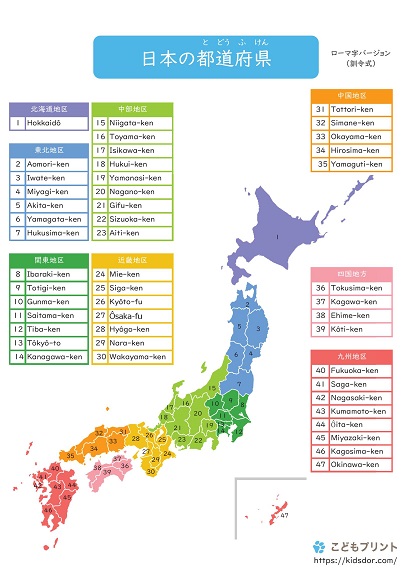



こどもプリント 都道府県をローマ字で覚えるプリント




小学4年生までに覚えたい 日本の都道府県 シグマベスト Amazon Com Books




記憶の回路を開く 都道府県を県番号込みで覚える 塾なしで医学部合格 地頭錬成法



都道府県 覚え方はこれで決まり 小学生 都道府県の簡単な覚え方3選 スマイルライフ お得なくらしのレシピ




都道府県名の覚え方と塾講師のナイショ話 育児書にない Asd母子の育児 お勉強 歴史の授業




小学生向け都道府県の簡単な覚え方5選 これなら1日で覚えられる 子供の習い事の体験申込はコドモブースター



都道府県の覚え方 一覧 キャラクターとマンガの日本地図 都道府県らくがき
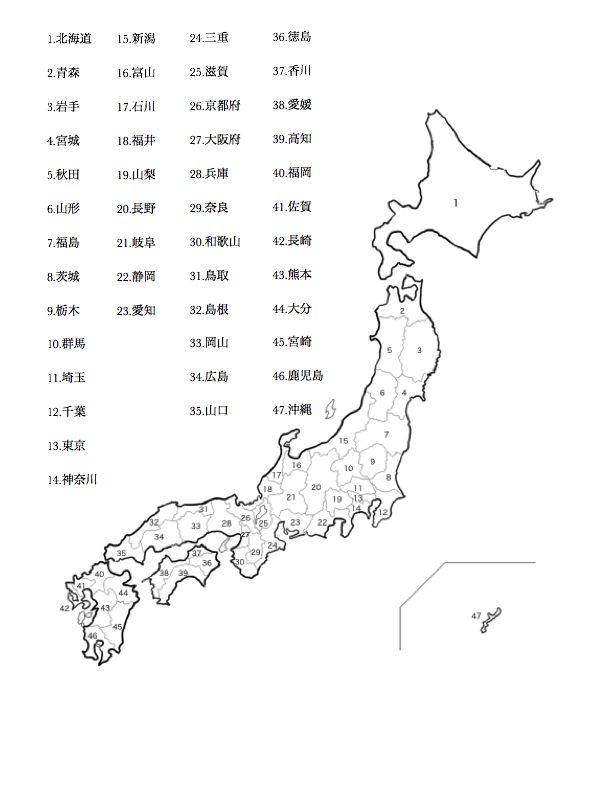



記憶の回路を開く 都道府県を県番号込みで覚える 塾なしで医学部合格 地頭錬成法




日本地図の覚え方 47都道府県 県庁所在地 県の形 Youtube




都道府県と県庁所在地を覚えよう 家庭学習レシピ
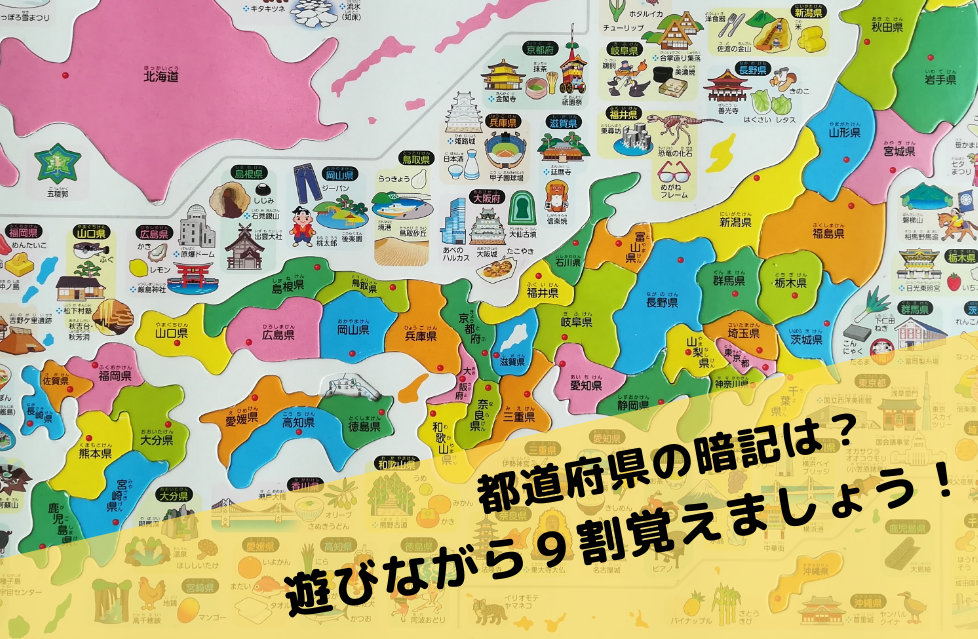



都道府県の効果的な覚え方は 遊びながら9割マスターしましょう よつなび




都道府県の漢字の覚え方 無料プリントで3ステップ Studywith 親子の学びブログ
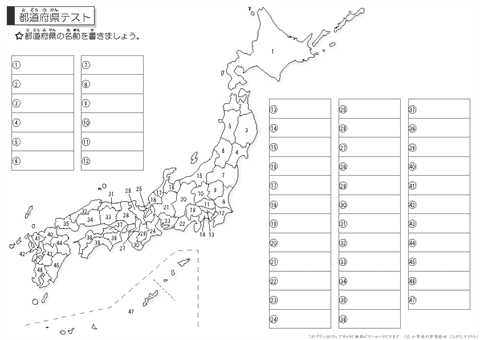



都道府県 県庁所在地 地方区分 テスト ちびむすドリル 小学生




ボード 脳トレ のピン



47都道府県の覚え方 子どもも簡単に覚えられる5つの方法 Chiik



暗記力のカベ 47都道府県はこうすれば無理なく覚えられる ベネッセ教育情報サイト




都 道府県 クイズ



大至急 明日 都道府県テスト 語呂合わせで一番早く覚える 都道府県らくがき



都道府県の覚え方 朝塾
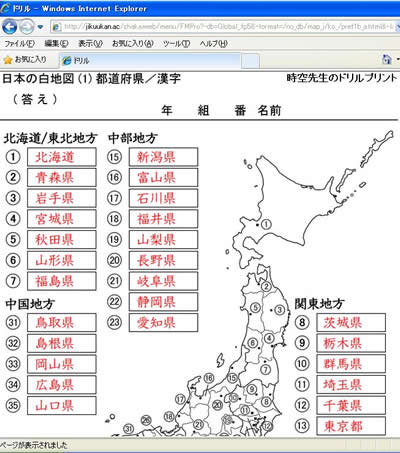



都道府県 県庁所在地を漢字で覚えよう 時空先生のドリルプリント




都道府県の覚え方 ゲームやクイズで覚える子供向けアプリの口コミ体験談 Studywith 親子の学びブログ




簡単暗記 都道府県の楽しい覚え方 絵 歌 語呂合わせ 都道府県らくがき 都道府県 らくがき 絵




都道府県の覚え方 語呂合わせや歌で覚える方法 Studywith 親子の学びブログ 覚える 学び 都道府県
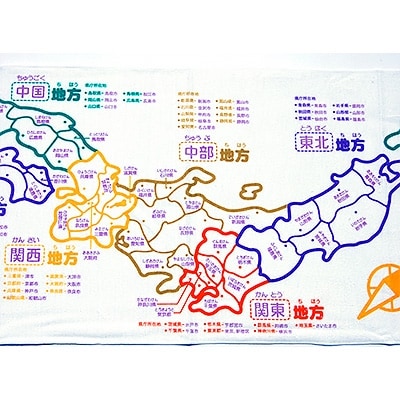



光で変わる 日本地図でおぼえる都道府県タオル 知育タオル お礼品詳細 ふるさと納税なら さとふる




親勉 地理 都道府県の形の覚え方 兵庫 親勉 3姉妹母さんの 子育てのピンチをチャンスに変える 家庭学習法 伊丹 西宮 尼崎



小学生版 1日10分日本地図をおぼえる本のページ あきやまかぜさぶろう コドモエのえほん 白泉社




都道府県の覚え方 歌 語呂合わせ アプリ ゲームで簡単に記憶しよう
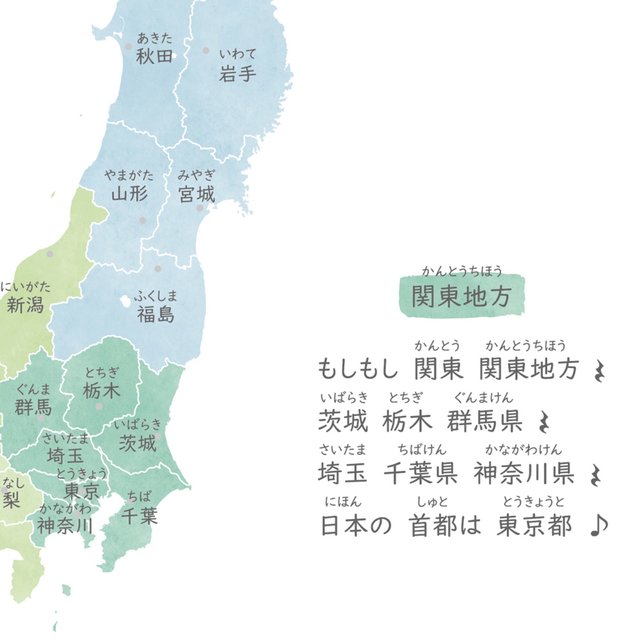



日本地図 歌って覚える都道府県 ハンドメイドマーケット Minne
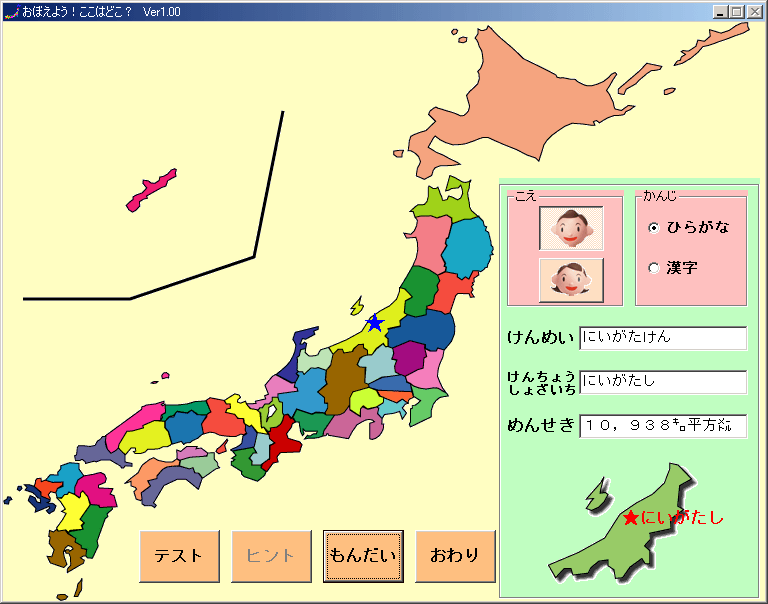



窓の杜 News 子ども向けの都道府県学習ソフト おぼえよう ここはどこ V1 00が公開




日本地図ゲーム 都道府県テスト 無料で楽しく学べる学習サイト 子供とインターネット All About



大至急 明日 都道府県テスト 語呂合わせで一番早く覚える 都道府県らくがき
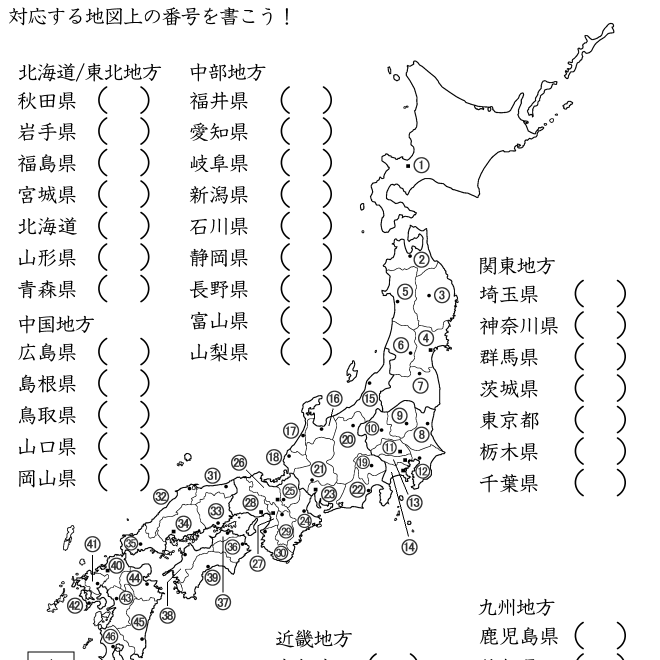



都道府県名を覚えるためのプリント 塾の先生が作った本当に欲しいプリント 楽天ブログ




都道府県と県庁所在地を覚えよう 家庭学習レシピ




県庁所在の覚え方と県庁所在に関する雑学などの紹介 Start Point




日本地図の覚え方 47都道府県をカンタンに覚えるコツとは 家庭教師のノーバス



Nitter By Pussthecat Org



完全版 県庁所在地の覚え方 語呂合わせ ダジャレで簡単 都道府県らくがき
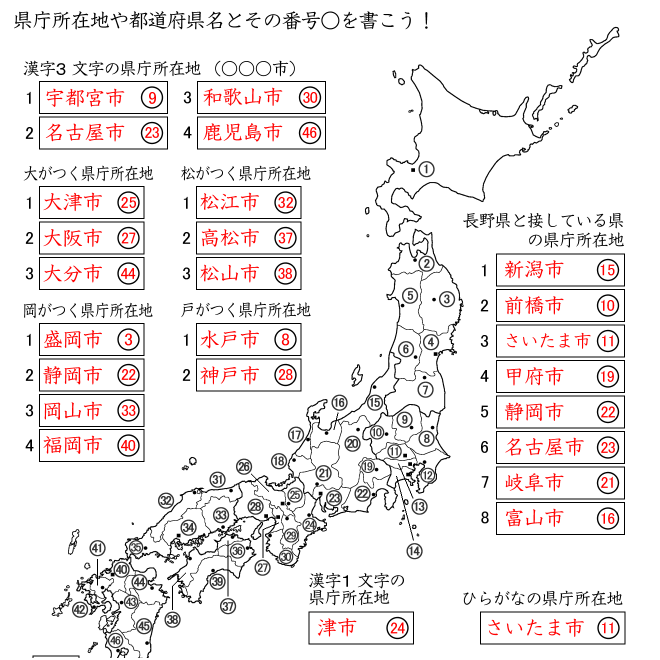



都道府県名を覚えるためのプリント 個人塾 個人指導の教材




日本地図があっという間に頭に入る 漢字 と 都道府県 の覚え方
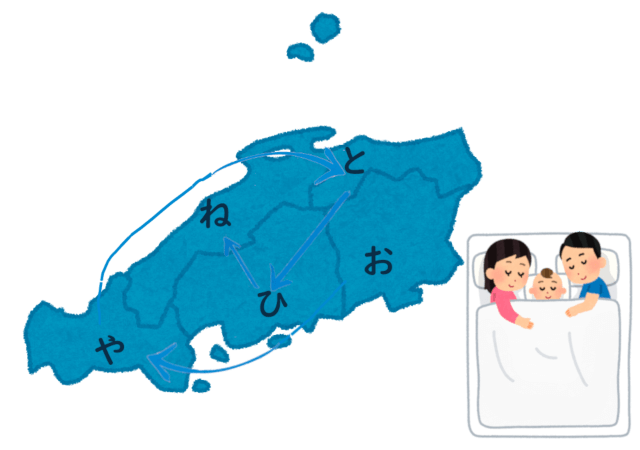



都道府県の覚え方にはコツが必要 おすすめ本と語呂合わせを紹介 バレエ男子の中学受験への日々
コメント
コメントを投稿